COMPUTATIONAL MODELLING OF TONALITY PERCEPTION
We are developing a computational model of the psychoacoustic factors underlying our perception of tonal harmony. The eventual aim is to provide a parsimonious and context-free theory of tonal harmony—one that can explain, with established perceptual and cognitive principles, why specific progressions of tones, chords and keys serve the same musical function today as they did in the seventeenth century.
The model is a development of a pre-existing model that accurately (and highly significantly) predicts the degree of closure (resolution) produced by the last chord in a variety of three-chord progressions (Milne 2009). We hope the developed model can provide effective predictions of the feelings of expectation and resolution induced by chord progressions and key modulations. In an ongoing series of experiments, we are testing the model against participants' responses to musical stimuli.
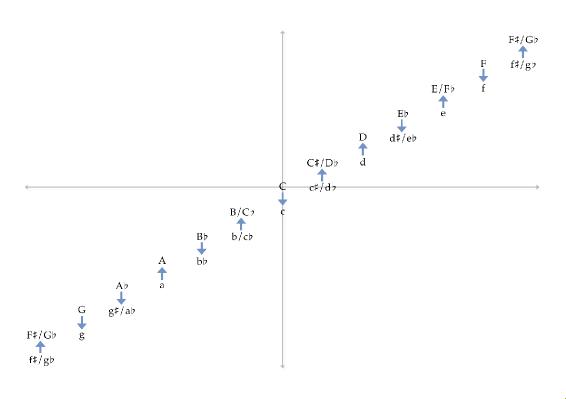
The model utilises two metrics: spectral pitch distance models the affinity of tones or chords (by comparing the frequencies of all their partials) (Milne et al. 2011); voice-leading distance models the pitch distance between tones or chords (by combining the pitch distances moved by all voices). Under the spectral pitch distance metric, some pairs of chords (e.g., C-maj and d-min) are closer (have greater affinity), while others (e.g., C-maj and D-maj) are more distant (have lower affinity). Because D-maj and d-min are close under the voice-leading metric, we hypothesise the latter is likely to be heard as an alteration of the former (the lower-affinity chord pair C-maj ↔ D-maj is likely to be heard as an alteration of the higher-affinity chord pair C-maj ↔ d-min). In the figure below, the voice-leading distance between all root-position triads is shown by their spatial distance; their spectral distance from a C-maj reference chord is shown by their colour (the darker the colour the closer). An alternative reference chord can be substituted.
(click to enlarge)
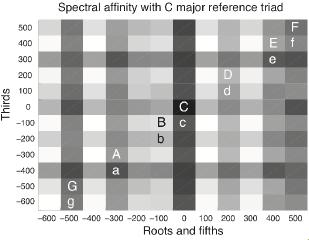
By observing all possible pairs of pairs of triads (note the intentional double use of "pairs" here!), we can model the probability that any given pair is heard as an alteration of another pair, and thus heard as active and in need of resolution. These relationships are summarised in the figure below. This figure assumes a C-maj chord has been played first. Each arrow points towards a chord that is likely to be heard as alterations of the chord at the foot of the arrow; for example, C-maj → D-maj is likely to be heard as an alteration of C-maj → d-min; or C-maj → E-maj is likely to be heard as an alteration of C-maj → e-min. A different reference triad can be substituted.
(click to enlarge)